TL;DR:

  • A method for learning expressive energy-based policies for continuous states and actions
  • Apply the method to learning maximum entropy policies
  • Used amortized Sten variational gradient descent to obtain complex multimodal policies
  • Improved exploration in the case of multimodal objectives
  • compositionality via pretraining general-purpose stochastic policies
  • There is a connection to actor-critic methods




Preliminaries


Maxmimum Entropy Reinforcement Learning

Maximum Entropy RL objective is

\[\begin{equation} \pi_\mathrm{MaxEnt}^* =\underset{\pi}{\mathrm{argmax}}\sum_t \mathbb E_{(s_t,a_t) \sim \rho_\pi} \left[\sum_{l=t}^\infty \gamma^{l-t} \mathbb E_{(s_l,a_l)} \left[r(s_t,a_t)+\alpha \mathcal H(\pi(\cdot|s_t)) \right]\right] \end{equation}\]

where \(\alpha\) is a temperature parameter that determines the relative importance of entropy and reward. This objective aims to maximize the entropy of the entire trajectory distribution for the policy \(\pi\). See more details of objective with discount factor in Appendix A.



Soft Value Functions and Energy-Based Models

General energy-based policies of the form

\[\begin{equation} \pi(a_t|s_t) \propto \mathrm{exp}(-\mathcal E(s_t,a_t)), \end{equation}\]

where \(\mathcal E\) is an energy function can represent very general class of distributions. There is a close connection between such energy-based models and soft versions of value functions and Q-functions, where we set \(\mathcal E(s_t,a_t) = \frac{1}{\alpha}Q_{soft}(s_t,a_t)\) and use the following theorem:


Theorem 1. Let the soft Q-function be defined by

\[\begin{equation}\label{eqn:soft-q} Q_{soft}^* (s_t,a_t)=r_t+\mathbb E_{(s_{t+1},...) \sim \rho_\pi} \left[\sum_{l=1}^\infty \gamma^l(r_{t+l}+\alpha \mathcal H(\pi_\mathrm{MaxEnt}^* (\cdot|s_{t+l})))\right], \end{equation}\]

and soft value function by

\[\begin{equation}\label{eqn:soft-value} V_{soft}^* (s_t)=\alpha \ \mathrm{log}\int_{\mathcal{A}} \mathrm{exp} \left( \frac{1}{\alpha} Q_{soft}^* (s_t,a') \right)\, da'. \end{equation}\]

Then the optimal policy for (2) is given by

\[\begin{equation}\label{eqn:opt-policy} \pi_\mathrm{MaxEnt}^* (a_t|s_t) = \mathrm{exp} \left(\frac{1}{\alpha} \left( Q_{soft}^* (s_t,a_t) - V_{soft}^* (s_t) \right) \right). \end{equation}\]

How to prove thm 1.:

  • If one rewrites the maximum entropy objective with soft Q-function, the discounted maximum entropy policy objective can be defined as
\[\begin{equation*} J(\pi) \triangleq \sum_t \mathbb E_{(s_t,a_t) \sim \rho_\pi} \left[Q_{soft}^\pi(s_t,a_t)+\alpha \mathcal H(\pi(\cdot|s_t))\right]. \end{equation*}\]
  • Check Appendix A.1 Theorem 4. Given a policy \(\pi\) , defining a new policy \(\tilde{\pi}\) as \(\tilde{\pi} \propto \mathrm{exp} (Q_{soft}^\pi (s, \cdot), \ \forall s\) maximize the objective \(\alpha \mathcal H(\pi(\cdot \mid s)+\mathbb E_{a \sim \pi} \left[ Q_{soft}^\pi (s,a)\right]\).
  • From theorem 4., by applying policy iteration \(\pi_{i+1}(\cdot \mid s) \propto \mathrm{exp}(Q_{soft}^{\pi_i}(s,\cdot))\) from an arbitrary policy \(\pi_0\) we can get \(\pi_\infty(a \mid s) \propto_a \mathrm{exp}(Q^{\pi_\infty}(s,a))\).


Theorem 2. The soft Q-function in (\ref{eqn:soft-q}) satisfies the soft bellman equation

\[\begin{equation} Q_{soft}^* (s_t,a_t)=r_t+\gamma \mathbb E_{s_{t+1} \sim p_s} \left[ V_{soft}^* (s_{t+1}) \right], \end{equation}\]

where the soft value function \(V_{soft}^*\) is given by (\ref{eqn:soft-val}).

How to prove thm 2.: check Appendix A.2.




Training Expressive Energy-Based Models via Soft Q-Learning


Soft Q-Iteration

Theorem 3. Soft Q-iteration. Let \(Q_{soft}(\cdot \mid \cdot)\) and \(V_{soft}(\cdot)\) be bounded and assume that \(\int_\mathcal{A} \mathrm{exp}\left(\frac{1}{\alpha}Q_{soft}(\cdot,a')\right)\, da' < \infty\) and that \(Q_{soft}^* < \infty\) exists. Then the fixed-point iteration

\[\begin{align} Q_{soft}(s_t,a_t) \gets r_t+\gamma \mathbb E_{s_{t+1} \sim p_s} \left[ V_{soft}(s_{t+1})\right], \quad \forall s_t, a_t \\ V_{soft}(s_t) \gets \alpha \ \mathrm{log} \int_\mathcal{A} \mathrm{exp}\left(\frac{1}{\alpha} Q_{soft}(s_t, a')\right)da', \quad \forall s_t \end{align}\]

converges to \(Q_{soft}^*\) and \(V_{soft}^*\) , respectively.

How to prove thm 3.: check Appendix A.2 that soft Bellman backup operator \(\mathcal T\) is a contraction.


PROBLEM

  1. Soft Bellman backup cannot be performed exactly in continuous or large state and action spaces.
  2. Sampling from the energy-based model in (\ref{eqn:opt-policy}) is intractable in general.



Soft Q-Learning

To handle problem 1, this paper express the Bellman backup process as a stochastic optimization. For soft value function, expectation via importance sampling is used(Algorithm 1 line 16-17, averaged over Kv samples).

\[\begin{equation}\label{eqn:prac-value} V_{soft}^\theta (s_t)=\alpha \ \mathrm{log} \mathbb E_{q_{a'}} \left[\frac{\mathrm{exp}(\frac{1}{\alpha} Q_{soft}^\theta (s_t,a'))}{q_{a'}(a')} \right]. \end{equation}\]

While \(q_{a'}\) can be an arbitrary distribution over the action space, the current policy is used in this paper. More details are in Appendix C.2.

For soft q-iteration, minimizing the following objective is used(Algorithm 1 line 18-19).:

\[\begin{equation} J_Q(\theta)=\mathbb E_{s_t \sim q_{s_t}, a_t \sim q_{a_t}} \left[ \frac{1}{2} \left(\hat Q_{soft}^{\bar{\theta}} (s_t,a_t)-Q_{soft}^\theta(s_t,a_t)\right)^2\right], \end{equation}\]

where \(q_{s_t}, q_{a_t}\) are positive over \(\mathcal S\) and \(\mathcal A\) respectively, \(\hat Q_{soft}^{\bar{\theta}} (s_t,a_t) =r_t+\gamma \mathbb E_{s_{t+1} \sim p_s} \left[ V_{soft}^\bar{\theta} (s_{t+1})\right]\) is a target Q-value, with \(V_{soft}^\bar{\theta} (s_{t+1})\) given by (\ref{eqn:prac-value}) and \(\theta\) being replaced by the target parameters, \(\bar{\theta}\) . While sampling distributions \(q_{s_t}\) and \(q_{a_t}\) can be arbitrary, real samples(=replay memories) are used in this paper.



Approximate Sampling and Stein Variational Gradient Descent (SVGD)

To handle problem 2, this paper used a sampling network based on Stein variational gradient descent (SVGD) and amortized SVGD. This sampling network has intriguing properties: 1) extremly fast sample generation, 2) accurate posterior distribution of an EBM and 3)analogous to actor-critic algorithm(Details in Appendix B). State-conditioned stochastic neural network \(a_t=f^\phi(\xi;s_t)\) , parametrized py \(\phi\) , that maps noise samples \(\xi\) is the form of network. The induced distribution of the actions are denoted as \(\pi^\phi(a_t \mid s_t)\) , and the objective is to find parameters \(\phi\) so that the induced distribution approximates the energy-based distribution in terms of the KL divergence

\[\begin{equation} J_\pi(\phi;s_t)=\mathrm{D_KL}\left(\pi^\phi(\cdot \mid s_t)\ \Vert \ \mathrm{exp} \left(\frac{1}{\alpha}\left(Q_{soft}^\theta(s_t,\cdot)-V_{soft}^\theta \right)\right)\right). \end{equation}\]

SVGD provides the optimal direction in the reproducing kernel Hilbert space of \(\kappa\) as \(\delta f^\phi\) (Algorithm 1. line 21-23, averaged over M sample actions, total K action sets):

\[\begin{equation} \Delta f^\phi(\cdot;s_t)=\mathbb E_{a_t \sim \pi^\phi} \left[ \kappa(a_t, f^\phi(\cdot;s_t)) \nabla_{a'}\ Q_{soft}^\theta(s_t,a') \mid_{a'=a_t} +\ \alpha \nabla_{a'} \ \kappa(a',f^\phi(\cdot;s_t))\mid_{a'=a_t} \right]. \end{equation}\]

By the assumtion \({\partial J_\pi \over\partial a_t} \propto \Delta f^\phi\), we can use the chain rule and backpropagate SVGD into policy network according to (Algorithm 1. line 24-25, averaged over K action sets)

\[\begin{equation} {\partial J_\pi (\phi;s_t) \over \partial \phi} \propto \mathbb E_\xi \left[ \Delta f^\phi(\xi;s_t) {\partial f^\phi(\xi;s_t) \over \partial \phi} \right]. \end{equation}\]

Details of updating policy parameters are described in Appendix C.1.



Algorithm Code & Additional Info

Figure from Reinforcement Learning with Deep Energy-Based Policies

IMO, target policy parameters \(\bar{\phi}\) are intended to sample an action in line 7.

update_interval in line 27 freezes target parameters to stabilize training.




Experiments

What to Figure Out ?

  1. Does their soft Q-learning method accurately capture a multi-modal policy distribution?
  2. Can soft Q-learning with energy-based policies aid exploration for complex tasks that require tracking multiple modes?
  3. Can a maximum entropy policy serve as a good initialization for fine-tuning on different tasks, when compared to pretraining with a standard deterministic objective?

Didactidc Example: Multi-Goal Environment

Figure from Reinforcement Learning with Deep Energy-Based Policies

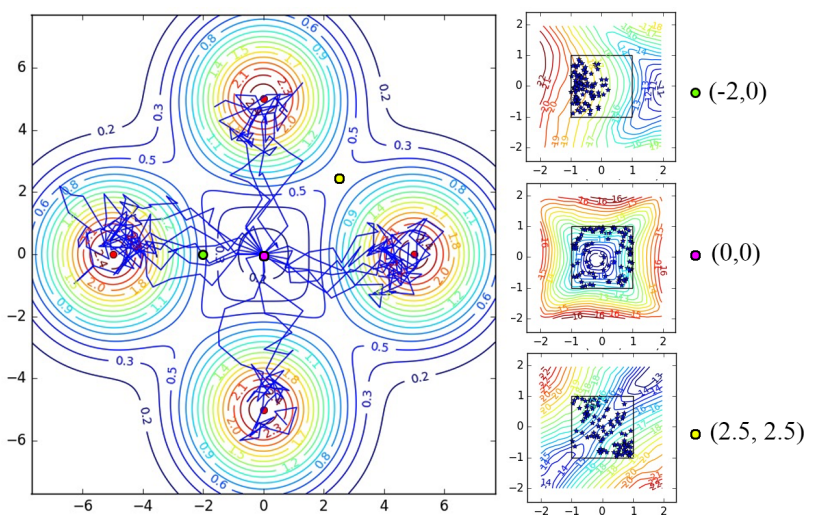
Illustration of 2D multi-goal environment. Left: trajectories from a policy learned with soft Q-learning. Right: Q-values at three selected states and 2D velocity of action samples. The stochastic policy samples actions closely following the energy landscape, hence learning diverse trajectories that lead to all four goals. In comparison, a policy trained with DDPG randomly commits to a single goal.



Learning Multi-Modal Policies for Exploration

Figure from Reinforcement Learning with Deep Energy-Based Policies

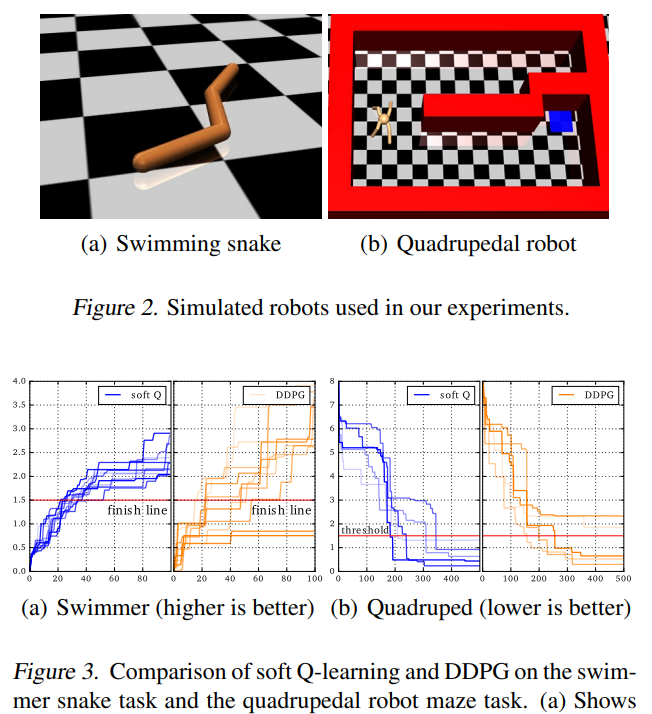
During the learning process, it is often best to keep trying multiple available options until the agent is confident that one of them is the best. The results on swimmer snake task and the quadrupedal robot maze task show that all runs of Soft Q-Learning method cross the threshold line, acquiring the more optimal strategy, while some runs of DDPG do not.



Accelerating Training on Complex Tasks with Pretrained Maximum Entropy Policies

Aims to find out how energy based policies can be trained with fairly broad objectives to produce an initializer for more quickly learning more specific tasks. The pretraining phase involves learning to locomote in an arbitrary direction, with a reward that simply equals the speed of the center of mass. Details of the pretraining are described in Figure 7 in Appendix D.3.

figure from Reinforcement Learning with Deep Energy-Based Policies

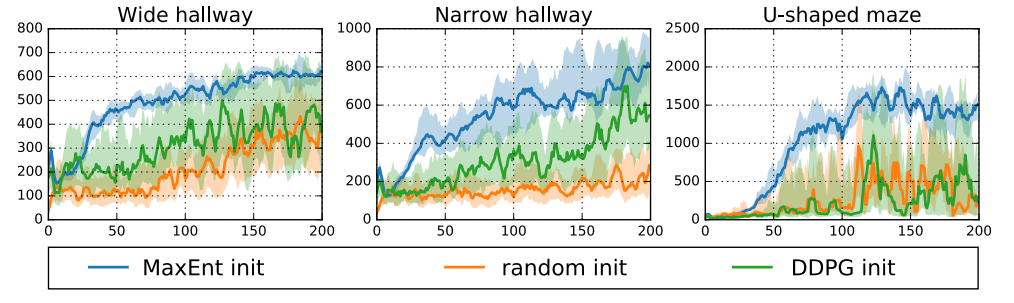
As the plots show, the pretrained policy gives a good initialization to learn the behaviors in the test environments more quickly than training a policy with DDPG from a random initialization.