TL;DR:

  • PEARL decouples the problems of inferring the task and solving it, allowing for off-policy meta-learning while minimizing mismatch between train and test context distributions.
  • With posterior sampling on latent context variable on which the policy is conditioned, PEARL can conduct temporally extended exploration to adapt unseen tasks rapidly.
  • Permutation-invariant encoder for the latent context variable allows decomposing a trajectory into a collection of single transitions.
  • To train context variable in a on-policy manner, context sampler \(\mathcal S_c\) samples recently collected data retaining on-policy performance with better efficiency.
  • PEARL outperforms prior algorithms in sample efficiency by 20-100X as well as in asymptotic performance by 50-100% in five of six domains.




Introduction


Meta-RL problems

Modern meta-learning is predicated on the assumption that the distribution of data used for adaptation will match across meta-testing and meta-test. As on-policy data will be used to adapt at meta-test time, on-policy data should be used during meta-training time as well. This makes algorithms exceedingly inefficient during meta-training and makes them inherently difficult to meta-train a policy to adapt using off-policy data.



How to tackle the problem ?

To achieve both meta-training efficiency(off-policy) and rapid adaptation(task inference), they integrate online inference of probabilistic context variables with existing off-policy RL algorithms. During meta-training, PEARL learns a probabilistic encoder that accumulates the necessary statistics from past experience into the context variables. At meta-test time, trajectories are collected with sampled context variables(=”task hypotheses”) and the collected trajectories update the posterior over the context variables, achieveing rapid trajectory-level adaptation.

Disentangling task inference from action makes PEARL particularly amenable to off-policy meta-learning; the policy can be optimized with off-policy data while the probabilistic encoder is trained with on-policy data to minimize distribution mismatch between meta-train and meta-test.



Experiments summary

Probabilistic embeddings for actor-critic RL (PEARL) achieves state-of-the-art results with 20-100X improvement in meta-training sample efficiency and substantial increases in asymptotic performance over prior state-of-the-art on six continuous control meta-learning environments. They further examine how PEARL conducts structured exploration to adapt rapidly to new tasks in a 2-D navigation environments with sparse rewards.





Meta-learning

Context-based meta-RL

  • Prior works with recurrent and recursive meta-RL method adapt to new tasks by aggregating experience into a latent representation on which the policy is conditioned. (whole experience = task specific context)
  • However, PEARL represents task contexts with probabilistic latent variables, enabling reasoning over task uncertainty.
  • Instead of using recurrence, PEARL leverages the Markov property in the permutation-invariant encoder to aggregate experience, enabling fast optimization especially for long-horizon tasks while mitigating overfitting.

Gradient-based meta-RL

  • Gradient-based meta-RL methods focus on on-policy meta-learning as off-policy data is non-trivial to do with policy gradient methods.
  • They found that PEARL (context-based method) is able to reach higher asymptotic performance, in comparison to methods using policy gradients.

Motivation of permutation-invariant encoder

  • Permutation-invariant embedding function described in this paper is inspired by the embedding function of prototypical networks.
  • While they use a distance metric in a learned, deterministic embedding space to classify new inputs, embeddings in this paper is probabilistic and is used to condition the behavior of an RL agent.



Probabilistic meta-learning

  • Probabilistic latent task variables: used to adapt model predictions for supervised learning <- extend this idea to off-policy meta-RL !
  • PEARL infers task variables and explores via posterior sampling.



Posterior sampling

  • In classical RL, posterior sampling maintains a posterior over possible MDPs and enables temporally extended exploration by acting optimally according to a sampled MDP.
  • PEARL: meta-learned variant of this method; probabilistic context captures the current uncertainty over the task, allowing the agent to explore in new tasks in a similarly structured manner.



Partially observed MDPs

  • Adaptation at test time in meta-RL can be viewed as a special case of RL in a POMDP:
\[\tilde{\mathcal M} = \left\lbrace \mathcal{\tilde{S}, A, \tilde{O}, \tilde{P}, E, r} \right\rbrace \quad \text{where} \quad \mathcal{\tilde{S} = S \times Z}, \tilde{s} = (s,z) \ \text{and} \ \mathcal{\tilde{O} = S}, \tilde o = s\]
  • The explicit state estimation \(p(s_t \mid o_{1:t})\) from POMDP can be written as task inference \(\hat p(z_t \mid s_{1:t},a_{1:t},r_{1:t})\) , where posterior sampling is used for exploration in new tasks.
  • Variational approach related to the prior work on solving POMDPs is used to estimate belief over task.




Problem Statement


  • Assume a distribution of tasks \(p(\mathcal T)\) , where each task is a MDP.
  • A task is defined as \(\mathcal T = \left\lbrace p(s_0), p(s_{t+1} \mid s_t,a_t), r(s_t,a_t) \right\rbrace\) . Note that varying transition functions and varying reward functions constitute task distribution.
  • Context \(c\) is referred to the history of past transitions. Let \(c^{\mathcal T}_ n = (s_n, a_n, r_n, s_n')\) be one transition in the task \(\mathcal T\) so that \(c^{\mathcal T}_ {1:N}\) comprises the experience collected so far.
  • Entirely new tasks are drawn from \(p(\mathcal T)\) at test-time.




Probabilistic Latent Context


Modeling and Learning Latent Contexts

An amortized variational inference approach is used to train an inference network \(q_\phi (z \mid c)\) , parameterized by \(\phi\) , that estimates the posterior \(p(z \mid c)\) . Let’s first check how variational inference approach works in VAE.


How variational inference approach works in VAE ?

Figure from [Source](https://imgur.com/PhHb2aF)

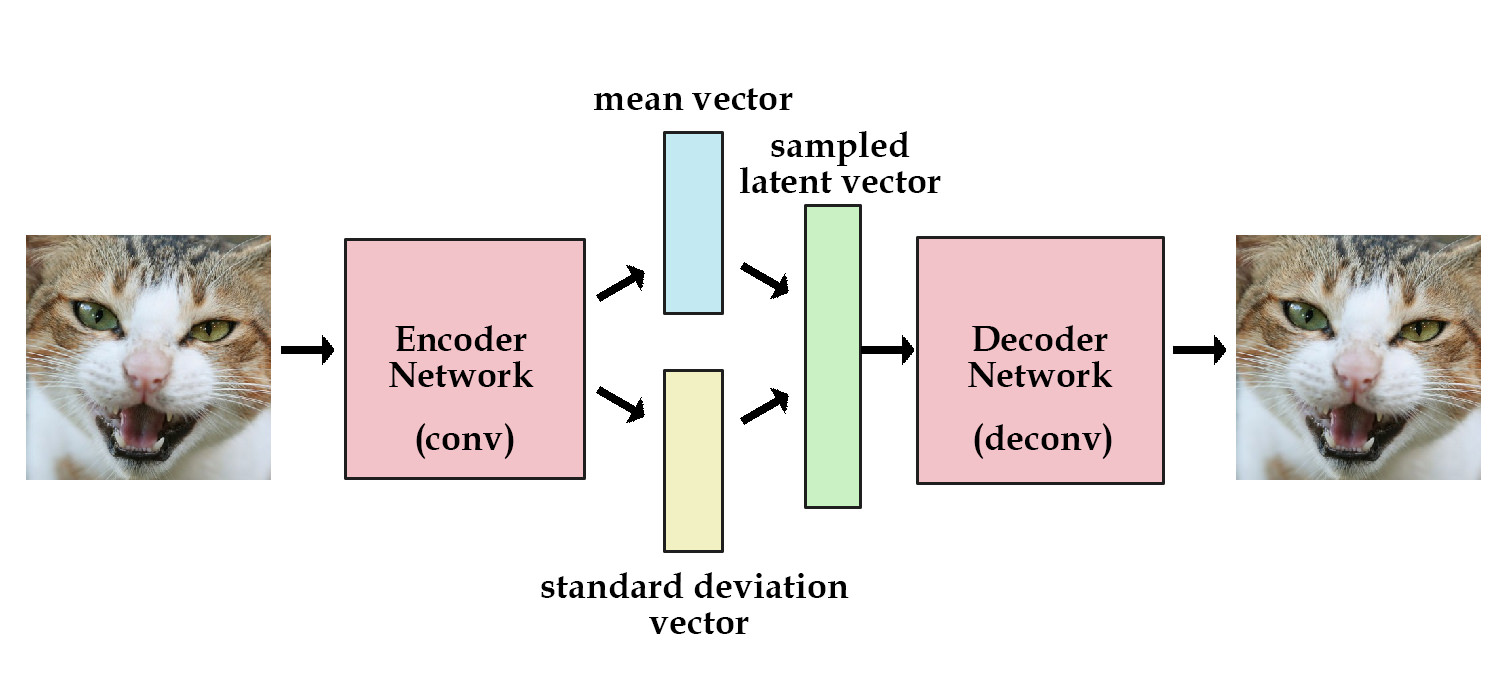
To estimate VAE parameters with maximal likelihood method, we need to maximize marginal log-likelihood \(\mathrm{log} p(x) = \mathcal{log} p(x \mid z)\ p(z)\) . As it is hard to calculate, we approximate the distribution \(p(z)\) to tractable distribution \(q(z \mid x)\) , which is called a variational inference. The evidence lower bound (ELBO) is calculated as RHS of the (\ref{eqn:ELBO}).

\[\begin{equation}\label{eqn:ELBO} \mathrm{log}\ p(x) \geq \mathbb E_{z \sim q(z \mid x)} \left[ \mathrm{log}\ p(x \mid z) \right] - \mathrm{ D_{KL}} (q(z \mid x) \parallel p(z)) \end{equation}\] \[\begin{align*} \text{proof)}\ \mathrm{log}\ p(x) & = \int q(z \mid x) \mathrm{log}\ \frac{p(x,z)}{q(z \mid x)}\, dz - \int q(z \mid x) \mathrm{log}\ \frac{p(z \mid x)}{q(z \mid x)}\, dz \\ & = \int q(z \mid x) \mathrm{log}\ \frac{p(x,z)}{p(z)}\, dz + \int q(z \mid x) \mathrm{log}\ \frac{p(z)}{q(z \mid x)}\, dz - \int q(z \mid x) \mathrm{log}\ \frac{p(z \mid x)}{q(z \mid x)}\, dz \\ & = \mathbb E_{z \sim q(z \mid x)} \left[ \mathrm{log}\ p(x \mid z) \right] - \mathrm{D_{KL}} (q(z \mid x) \parallel p(z)) + \mathrm{D_{KL}} (q(z \mid x) \parallel p(z \mid x)) \end{align*}\]

By maximizing the ELBO which is easy to calculate, we can maximize marginal log-likelihood \(\mathrm{log} p(x)\) . As the objective function used in deep learning is loss function, we can rewrite (\ref{eqn:ELBO}) as (\ref{eqn:Loss}).

\[\begin{equation}\label{eqn:Loss} L = - \mathbb E_{z \sim q(z \mid x)} \left[ \mathrm{log}\ p(x \mid z) \right] + \mathrm{ D_{KL}} (q(z \mid x) \parallel p(z)) \end{equation}\]

Specifically, \(- \mathbb E_{z \sim q(z \mid x)} \left[ \mathrm{log}\ p(x \mid z) \right]\) is a reconstruction term that calculates the cross-entropy between encoder and decoder. \(\mathrm{D_{KL}} (q(z \mid x) \parallel p(z))\) is a regularization term that constrains \(q(z \mid x)\) to be similar to the prior \(p(z)\) (can be any tractable distribution). Meanwhile, maximizing the ELBO is equivalent to minimizing the difference between posterior \(p(z \mid x)\) and its estimation \(p(z \mid x)\).


Applying this idea to meta-RL problem

As minimizing the KL divergence between the posterior \(p(z \mid c)\) and the inference network \(q_\phi (z \mid c)\) can be achieved by maximizing the ELBO, we can define the variational lower bound loss:

\[\begin{equation}\label{eqn:inf-net} \mathbb E_{\mathcal T} \left[ \mathbb E_{z \sim q_\phi (z \mid c^{\mathcal T})} \left[ R(\mathcal T, z) + \beta\ \mathrm{D_{KL}}\left(q_\phi(z \mid c^{\mathcal T}) \parallel p(z) \right) \right]\right] \end{equation}\]

where \(p(z)\) is a unit Gaussian prior over \(Z\) and \(R(\mathcal T, z)\) could be a variety of objectives, such as reconstructing the MDP, modeling the state-action value functions or maximizing returns through the policy over the distribution of tasks. The KL divergence term can also be interpreted as the result of a variational approximation to the information bottleneck that constrains \(z\) to contain only information from the context that is necessary to adapt to the task at hand, mitigating overfitting to training tasks (by Lagrange multiplier \(\beta\) .


Designing the architecture of the inference network

An encoding of a fully observed MDP should be permutation invariant: the order of a collection of transitions \(\left\lbrace s_i, a_i, s_i', r_i \right\rbrace\) doesn’t matter when used to encode MDP (task inference, value function, etc.). (Because, a single transition contains all the information that makes task distribution: transition function, reward function) With this observation, a product of independent factors consitutes permutation-invariant inference network \(q_\phi(z \mid c_{1:N})\) as

\[\begin{equation} q_\phi(z \mid c_{1:N}) \propto \prod_{n=1}^N \Psi_\phi(z \mid c_n). \end{equation}\]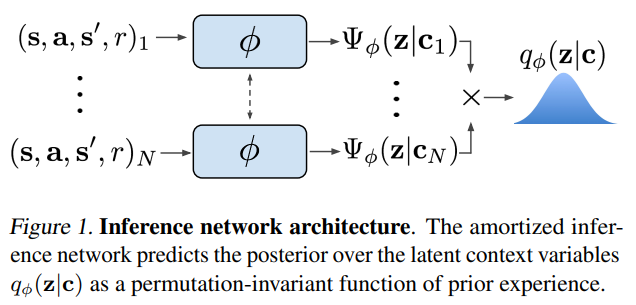
Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"

To keep the method tractable, they use Gaussian factors \(\Psi_\phi(z \mid c_n) = \mathcal N (f_\phi^\mu (c_n), f_\phi^\sigma (c_n))\) , which result in a Gaussian posterior.



Posterior Sampling and Exploration via Latent Contexts

Modeling the latent context as probabilistic allows us to make use of posterior sampling for efficient, temporally extended exploration at meta-test time. In this paper, PEARL directly infers a posterior over the latent context \(Z\) , which may encode the MDP itself if optimized for reconstruction, optimal behaviors if optimized for the policy, or the value function if optimized for a critic (actual implementation of PEARL as (\ref{eqn:critic-loss})). During meta-training, the prior distribution over tasks is captured with training tasks and also learns to efficiently use experience to infer new tasks. At meta-test time, \(z\) is sampled from the prior and a trajectory is collected according to \(z\) . Then using the collected experience to update the posterior and continue exploring coherently in a manner that acts more and more optimally as our belief narrows.




Off-Policy Meta-Reinforcement Learning


There has been two challenges to design off-policy meta-RL algorithms:

  • The distribution of data used for adaptation need to match across meta-training and meta-test. (Lead to data inefficiency during meta-training)
  • Meta-RL requires the policy to reason about distributions (over tasks, states and actions) , so as to learn effective stochastic exploration strategies. (Using value-based RL in meta-learning is ineffective, especially in reasoning about task during meta-test)

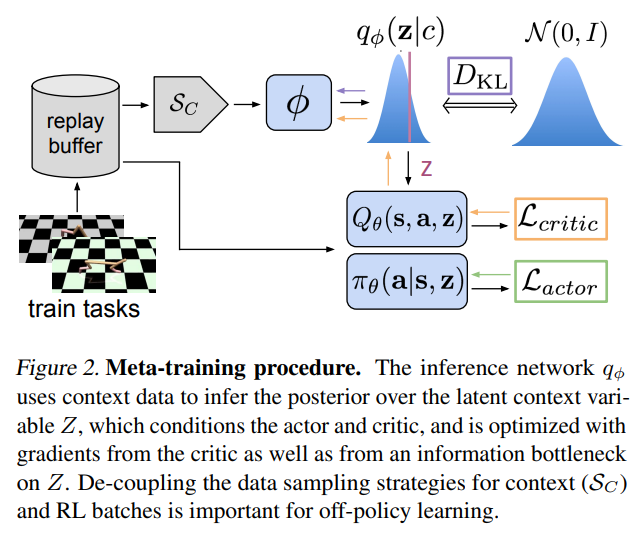
The main insight in designing an off-policy meta-RL method with the probabilistic context is that the data used to train the encoder need not be the same as the data used to train the policy. The policy can treat the context \(z\) as part of the state in an off-policy RL loop (as task inference is the only on-policy process that needs distribution match of data), while the stochasticity of the exploration process is provided by the uncertainty in the encoder \(q(z \mid c)\) (on-policy task inference via posterior sampling). The actor and critic are always trained with off-policy data from the entire replay buffer \(\mathcal B\) . However, the encoder is trained with context batches sampled from a sampler \(\mathcal S_c\) , where \(\mathcal S_c\) is sampled from a replay buffer of recently collected data retains on-policy performance with better efficiency. (An in-between strategy between off-policy \(\mathcal S_c\) and strict on-policy \(\mathcal S_c\))

The training procedure is summarized in Figure 2 and Algorithm 1. Meta-testing is described in Algorithm 2.

Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"
Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"



Implementation

  • Algorithm is built on top of the soft actor-critic algorithm (SAC).
  • Parameters of the inference network \(q(z \mid c)\) , actor \(\pi_\theta(a \mid s, z)\) and critic \(Q_\theta(s,a,z)\) are optimized jointly as Figure 2 with reparameterization trick on sampling context variable \(z\) .
  • Inference network is trained to encode the value function using gradients from the Bellman update for the critic (line 19 of Algorithm 1).
  • The critic loss and the actor loss are written as
\[\begin{align}\label{eqn:critic-loss} & \mathcal L_{\mathrm{critic}} = \mathbb E_{(s,a,r,s') \sim \mathcal B, z \sim q_\phi(z \mid c)} \left[ Q_\theta(s,a,z) - (r+\bar{V}(s',\bar{z}))\right]^2 \\ & \mathcal L_{\mathrm{actor}} = \mathbb E_{s \sim \mathcal B, a \sim \pi_\theta, z \sim q_\phi(z \mid c)} \left[ \mathrm{D_{KL}} \left( \pi_\theta(a \mid s, \bar{z}) \parallel \frac{\mathrm{exp} (Q_\theta(s,a,\bar{z}))}{\mathcal Z_\theta(s)} \right)\right] \end{align}\]

where \(\bar{V}\) is a target network and \(\bar{z}\) indicates that gradients are not being computed through it (as a computational graph on Figure 2).

  • The context data sampler \(\mathcal S_c\) samples uniformly from the most recently collected batch of data (line 13 of Algorithm 1).
  • The batch of data \(\mathcal B^i\) is recollected every 1000 meta-training optimization steps.




Experiments


Sample Efficiency and Performance


Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"

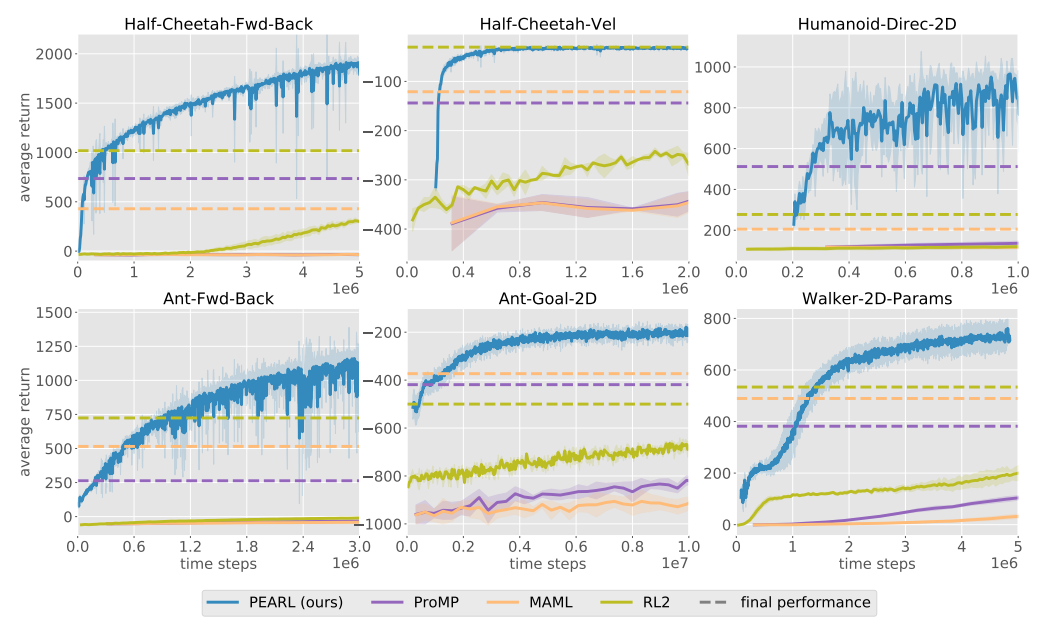
Experimental Setup.

  • 6 locomotion task families require adaptation across reward functions or across dynamics.
  • Baseline algorithms: gradient-based(ProMP, MAML-TRPO), recurrence-based( with PPO)
  • Attempted to adapt recurrent DDPG, but not work (due to the distribution mismatch in the adaptation data and the difficulty of training with trajectories rather than decorrelated transitions)


Results. PEARL uses 20-100x fewer samples during meta-training than previous meta-RL approaches while improving final asymptotic performance by 50-100% in five of six domains.



Posterior Sampling For Exploration


Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"
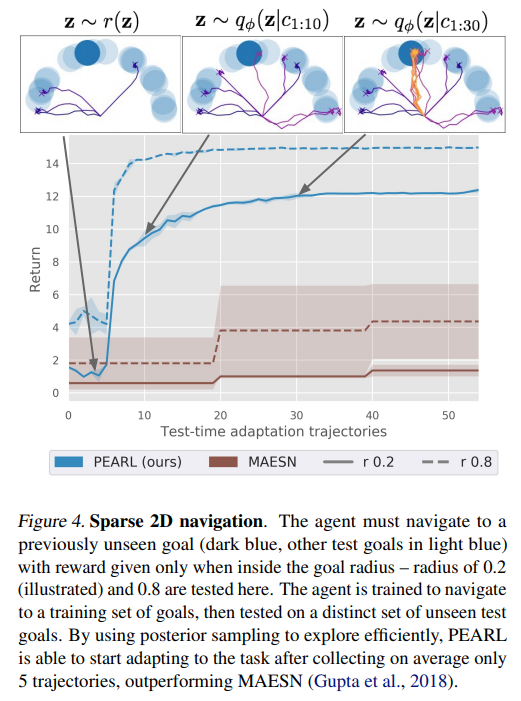
  • While they aim to adapt to new tasks with spare rewards, meta-training with sparse rewards is expremely difficult. For simplicity they assume access to the dense reward (the negative distance to the goal as the reward) during meta-training, as done by MAESN.
  • MAESN : models probabilistic task variables, performs on-policy gradient-based meta-learning
  • PEARL can adapt to the new sparse goal in fewer trajectories and also outperforms MAESN in terms of final performance.
  • PEARL is also more efficient during meta-training.



Ablations


Figure from "Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables"

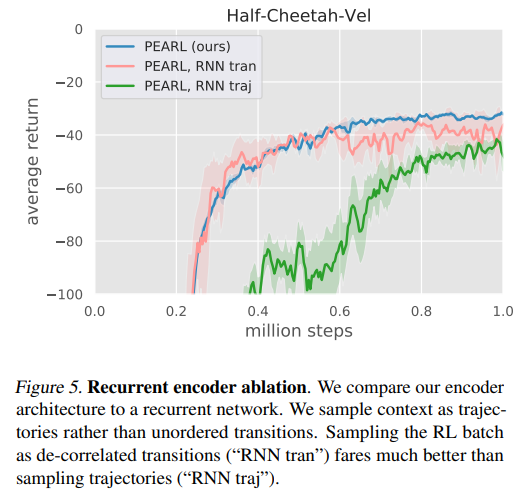
Inference network architecture.

  • Compare permutation-invariant encoder for the latent context \(Z\) to RNN encoder. There are two options for sampling the RL batch: 1) unordered transitions as in PEARL (“RNN tran”) 2) sets of trajectories (“RNN traj”)
  • “RNN tran” results in comparable performance to PEARL, at the cost of slower optimization.
  • “RNN traj” results in steep drop in performance.
  • The result demonstrates the importance of decorrelating the samples used for the RL objective.


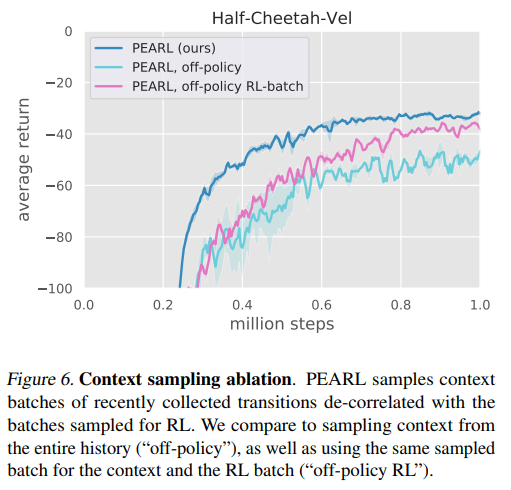
Data sampling strategies.

  • Ablate the context sampling strategy used during training. Three options for \(\mathcal S_c\) are: 1) original : sample recently colleted data, distinct from the RL batch 2) “off-policy” : sample fully off-policy data, distinct from the RL batch 3) “off-policy RL-batch” : sample fully off-policy data, identical to the RL batch
  • The results demonstrates the importance of careful data sampling in off-policy meta-RL.


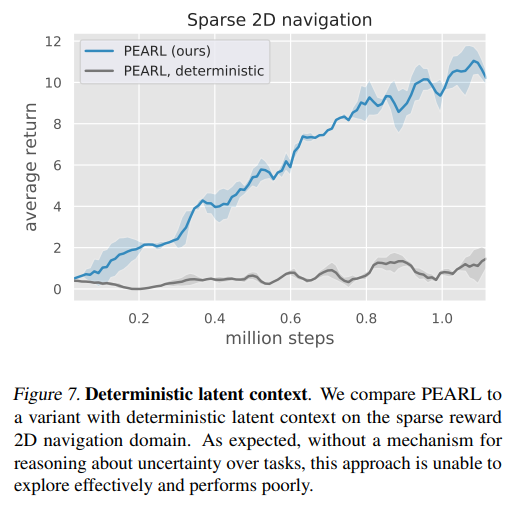
Deterministic context.

  • “deterministic” : let the distribution \(q_\phi (z \mid c)\) to a point estimate.
  • With no stochasticity in the latent context variable, the only stochasticity comes from the policy and is thus time-invariant, hindering temporally extended exploration.